Panorama Photo

Details
Location:	Marina di Campo auf Elba (2 m)	by:	Klaus Föhl
Area:	Italy	Date:	2018-05-30

Vergleich zweier Skalierungsverfahren bei einem fast-360-Grad-Panorama, allerdings waren da die Schiffsaufbauten ein wenig im Weg gewesen.

Ich habe ein Vergleichsbild eingefügt. Das große Bild ist im linearen Farbraum skaliert, das kleine Bild im nichtlinearen sRGB-Raum. Den Unterschied sieht man an dünnen Linien beispielsweise den Geländern.

Edit: das ursprüngliche Bild ist 20000x2000 Pixel. Skaliert habe ich so:
convert bild1.jpg -colorspace RGB -filter lanczossharp -distort resize 5000x500 -colorspace sRGB bild2.jpg
beziehungsweise für das Bildmaterial des eingesetzten Bildes:
convert bild1.jpg -filter lanczossharp -distort resize 5000x500 bild3.jpg
Danach in gimp einen Ausschnitt von bild3 in bild2 eingesetzt, auf Bildgrenzen modulo 8 = 0 geachtet und mit unveränderter Quailität/Kompression abgespeichert.

Das Bild ohne insert ist Nummer 24245.

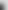You need to login to like or comment a panorama

Liked 1 times

Comments

Interessant dieser Vergleich, Klaus. Da tauchen aber gleich eine Menge von Fragen auf:
- Welchen Farbraum, der linear ist, hast Du benutzt?
- Ergaben sich die Unterschiede nur für die zuletzt besprochene Skalierung des Panoramabildes auf 500 px Höhe oder ergeben sich auch welche für andere Operationen?
..
- In welchem Farbraum hast Du denn die Einzelbilder gemacht bzw. aus RAW's transformiert?
..
Die Browser geben das Bild normalerweise nur in sRGB wieder. Spielt das für diesen Vergleich keine Rolle?

2018/09/14 22:23 , Heinz Höra

sRGB mit Gamma und linear

Auch wenn "convert" Bezeichnungen sRGB und RGB verwendet, findet alles im Farbraum sRGB statt. Der Unterschied ist die Kodierung der Helligkeitswerte in Zahlen. Die findet bei RGB linear statt, bei sRGB (fast exakt) mit Gamma=2.2 als Exponenten. Deswegen wechsle ich hin und her.

Falls ich in sRGB Pixel verschiedener Helligkeit mittele, indem ich das arithmetische Mittel der Zahlen berechne, ist die Helligkeit immer zu klein. Korrekt ist die Einzelwerte mit 2.2 zu potenzieren, dann zu mitteln, und zum Schluss die 2.2te Wurzel zu ziehen.

Wenn man das nicht macht, treten eben diese gestrichelten Linien auf. Ein helles Pixel bzw. zwei Pixel mit halbem Zahlenwert doch jeweils knapp 1/4 Leuchtstärke sind halt in der Summe unterschiedlich hell.

Ausgangsfoto für die Skalierung JPG. Ob ich anfangs mit RAW starte ist für den Effekt unerheblich. Und ja, das Auftreten des Effektes benötigt einen Monitor, der JPG -Bilder mit Gamma ungleich eins darstellt.

Prinzipiell tritt der Effekt auch beim Panorama berechnen in hugin auf. Wenn man aber direkt in hugin verkleinert, hat man dazu das noch gravierendere Problem der Unterabtastung.

2018/09/14 23:37 , Klaus Föhl

Danke, Klaus, für die Beantwortung meiner Fragen. Mal sehen, ob es mir gelingt, das alles richtig zu verstehen.

2018/09/15 10:43 , Heinz Höra

Mir gefällt das also Pano sehr gut - die Sternchen schon mal im Vorgriff auf eine Version ohne Bild im Bild. Die Gamma Diskussion haben wir hier noch nicht geführt. Aber hängt nicht alles dann auch von der Gamma-Einstellung von Betriebssystem und Monitor des Betrachters ab? VG Martin

2018/09/15 11:52 , Martin Kraus

Ja schau mer mal wie die finale Version aussehen wird. Bei allem theoretisiere hat doch das Einzelbild eine nach meinem Geschmack angenehme Schärfe, was beim Pano nicht so der Fall ist.

2018/09/16 13:55 , Steffen Minack

Ich kann Steffen hier nur zustimmen. Bei 500 Pixel Bildhöhe ist Vieles in puncto Bildqualität/Schärfe nur ein Kompromiss. Ich habe zunächst meine Panoramen auch mit IrfanView herunterskaliert. Letztendlich haben mich wie bereits erwähnt die mit ImageMagick erzielten Ergebnisse am meisten überzeugt.
Herzliche Grüße, Matthias.

2018/09/17 21:02 , Matthias Stoffels

Bild ohne insert ist Nummer 24245.

Wollte ich vollständigkeitshalber auch per Kommentar informieren.

2018/09/19 13:15 , Klaus Föhl